CIRCUNFERENCIA
DEFINICIÓN:
La circunferencia es un conjunto de puntos (x, y) en el plano cartesiano que equidistan a un punto fijo llamado centro. La distancia fija se le llama radio.
Ecuación Canónica:
Para una circunferencia de centro en el origen de coordenadas (h, k) = (0, 0) y radio R, la ecuación canónica es de la forma:
x2+y2=R2
PARÁBOLA
DEFINICIÓN:
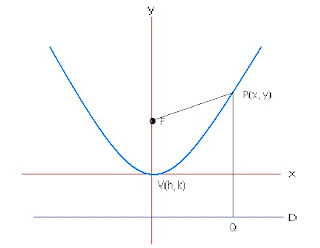
La parábola es un conjunto de puntos en el plano (x, y) que se encuentran a la misma distancia de un punto fijo F llamado foco y una recta D llamada directriz.
Los parámetros de la parábola son:
Vértice V (h, k): Donde la curva se divide en dos partes iguales.
Foco: F: El punto fijo a una distancia p del vértice, llamada distancia focal.
Eje de Simetría: Una recta que para por el vértice y es perpendicular a la directriz.
Directriz D: Recta ubicada a la misma distancia que el foco pero en sentido contrario.
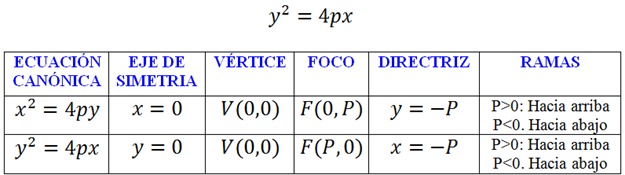
Ecuación Canónica: (Eje de Simetría vertical)
Toda parábola con eje de simetría vertical y vértice en el origen, tiene como ecuación canónica:
Ecuación Canónica: (Eje de Simetría horizontal)
Toda parábola con eje de simetría horizontal y vértice en el origen, tiene como ecuación canónica:
HIPÉRBOLA
DEFINICIÓN:
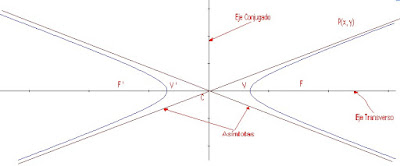
La Hipérbola es un conjunto de puntos en el plano (x, y) cuya diferencia a dos puntos fijos llamados focos es constante.
Los parámetros de la Hipérbola son:
Centro: C (h, k). Equidistante a los vértices
Vértices V y V’ Donde las curvas se dividen en dos partes iguales.
Focos: F y F’: Los puntos fijos.
Eje Transverso: Una recta que para por los vértices y por los focos.
Eje Conjugado: En una recta perpendicular al eje transverso y para por el centro.
Asíntotas: Dos rectas que paran por el centro delimitan las curvas de la hipérbola.
Ecuación Canónica: (Eje transverso horizontal)
Toda hipérbola con eje transverso paralelo al eje de las abscisas y centro en el origen de coordenadas, tiene como ecuación:
Ecuación Canónica: (Eje transverso vertical)
Toda hipérbola con eje transverso paralelo al eje de las ordenadas y centro en el origen de coordenadas, tiene como ecuación:
ASINTOTAS:
En la hipérbola se conocer dos rectas oblicuas que pasan por centro de la hipérbola, cuya función es orientan la curvatura de la figura. La obtención de la ecuación de dichas rectas, se hace a partir de la ecuación canónica. La obtención de la ecuación se hace despejando la variable y en la canónica.
Se presentan dos casos:
1. Eje transverso horizontal:
2. Eje transverso Vertical:
ELIPSE
DEFINICIÓN:
La elipse es un conjunto de puntos (x, y) en el plano cartesiano, tal que la suma de sus distancias a dos puntos fijos llamados focos, es constante.
Al igual que la circunferencia, la elipse tiene los parámetros que la caracterizan, los cuales se describen a continuación.
Los parámetros de la elipse son:
Centro: C (h, k)
Vértices mayores: V y V’
Vértices menores: u y u’
Focos: f y f’
Eje mayor: 2a (Distancia V V ‘)
Eje menor: 2b (Distancia u u ‘)
Por definición: 2a > 2b
Ecuación Canónica: (Con eje mayor en x)
La ecuación canónica de la elipse con centro en C (0, 0) y eje mayor sobre la coordenada x es de la forma:
Ecuación Canónica: (Con eje mayor en y)
La ecuación canónica de la elipse con centro en C (0, 0) y eje mayor sobre la coordenada y es de la forma:
EXCENTRICIDAD:
El concepto de excentricidad es usado para describir la forma de la curva, haciendo una relación de cociente entre la longitud del foco y la longitud del eje mayor. Esto nos permite determinar si la elipse es aplanada o abombada.
La excentricidad se define como:
Para la elipse la excentricidad está entre 0 y 1. (0 < e < 1). Cuando e→0 la elipse es casi circular, cuando e→1 la elipse es casi plana. (→Significa tiende o se acerca a...)
Para la circunferencia la excentricidad es cero (e = 0), esto significa que cuando e = 0, la figura es concéntrica. Lo anterior quiere decir que si a = b, entonces c = 0, obteniendo así una circunferencia.
Referencias bibliográficas
Rondón, J. (2017). Algebra, Trigonometría y Geometría Analítica. Bogotá D.C.: Universidad Nacional Abierta y a Distancia. Páginas 290 – 306. Recuperado de http://hdl.handle.net/10596/7689














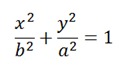


No hay comentarios.:
Publicar un comentario