EJEMPLOS DESARROLLADOS Y CONSTRUCCIONES EN GEOGEBRA PASO A PASO.

CIRCUNFERENCIA

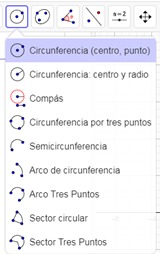
1. Obtener la ecuación de la circunferencia cuyo centro es el punto (6, 2) y su radio es 5

Solución:

Se capturan las coordenadas del centro, con la recomendación de llamar a este punto C. Posteriormente se selecciona la herramienta Circunferencia, opción Circunferencia (centro, radio) 

Al activar esta herramienta, GeoGebra solicita hacer clic en el centro e indicar el valor del radio.

Al dar el valor del radio, se observará la gráfica de la circunferencia y en la Vista Algebraica aparece la ecuación en la forma ordinaria, (x-6)² + (y-2)² = 25

Al activar el menú emergente en la ecuación ordinaria, se cuenta con la opción de cambiar a otra forma.

2. Obtener la ecuación de la circunferencia cuyo centro es el punto (4, -5) y que pasa por el punto (-1, 7)

Solución:

Se capturan las coordenadas de los dos puntos y se selecciona la herramienta Circunferencia (centro, punto). Posteriormente se hace clic en el centro y en seguida en el punto.

GeoGebra proporciona la gráfica y la ecuación:

3.3. Obtener la ecuación de la circunferencia en la que uno de sus diámetros tiene como extremos los puntos (5, -6) y (12, 17)

Solución:

Se capturan ambos puntos y se traza el segmento entre ellos.

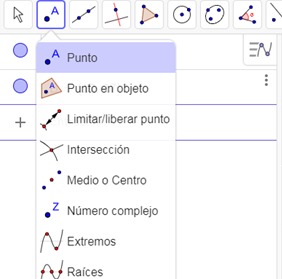
En la herramienta Punto se selecciona la opción Medio o Centro y se hace clic en el segmento o en los dos puntos extremos y GeoGebra proporciona las coordenadas del punto medio. 

Finalmente se utiliza la opción Circunferencia (centro, punto), haciendo clic, primero en el centro y después en cualquiera de los puntos extremos del diámetro.

4.4. Obtener la ecuación de la circunferencia cuyo centro es el punto A=(5, -4) y una de sus rectas tangentes tiene como ecuación 3x-7y=21

Solución:

Siguiendo el procedimiento del ejercicio, cuando se tienen las coordenadas del punto B, se utiliza la herramienta Circunferencia (centro, punto). 

Después de ocultar la gráfica de la recta perpendicular a la tangente, la gráfica queda como se muestra en la siguiente figura:

En la Vista Algebraica se presenta la ecuación buscada. (x-5)² + (y+4)² = 8.38

5. Obtener la gráfica de la circunferencia cuya ecuación es x²+y²=25 e indicar cuál es su centro. 

Solución:

Se captura la ecuación de la circunferencia, después de introducir la ecuación, la gráfica será como la siguiente: 

GeoGebra asignó el nombre c a esta circunferencia. Para obtener el centro se escribe en Entrada el comando centro(c) y en la Vista Algebraica se observan las coordenadas de éste, o sea el origen. 

PARÁBOLA

1. Obtener la gráfica de la parábola cuya ecuación es 

Solución:

·       Se captura la ecuación y se obtiene: 

2. Obtener el vértice, el foco, y la directriz de la parábola del ejercicio anterior.

Solución:

Considerando que GeoGebra asignó el nombre c a la parábola, se capturan los siguientes comandos, dando Enter, después de cada uno de ellos.

Vértices(c) = El comando es vértices (en plural y con acento)

Foco(c)

Directriz(c)

El resultado obtenido es foco (-8, 3), vértice (-5, 3) y directriz, la recta cuya ecuación es x = -2

Es posible cambiar el nombre de un punto o un elemento utilizando el menú emergente y la opción Renombra.

3. Obtener la gráfica de la parábola cuya ecuación es

x²+10x-24y+193=0

Solución:

·       Se captura la ecuación y se obtiene: 

4. Obtener la ecuación del eje focal de la parábola del problema anterior.

Solución:

En Entrada se introduce el comando Ejes(c) y GeoGebra presenta dos líneas rectas y sus ecuaciones. Como el eje focal es paralelo al eje Y, se deduce que la ecuación es x=-5 corresponde al eje buscado.

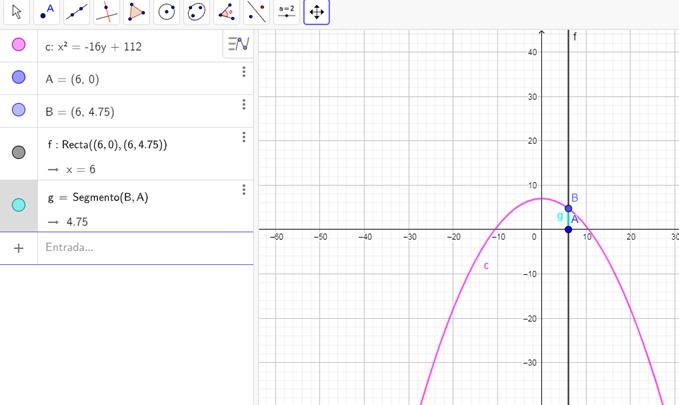
5. Determinar la distancia vertical entre el punto A=(6,0) y la parábola cuya ecuación es x²=-16(y-7)⇒⇒ x²=-16y+112

Solución:

·       Se introduce la ecuación de la parábola para obtener su gráfica

·       Se capturan las coordenadas del punto A

·       Se introduce la ecuación de la recta x=6

·       Se obtiene el punto de intersección entre la recta y la parábola

·       Se traza el segmento AB. La longitud de este segmento es la distancia buscada (b=4.75). 

HIPÉRBOLA

1.    Obtener la gráfica de la hipérbola cuya ecuación es y²/64 - x²/36 =1

Solución:

Se captura la ecuación en la forma y²/64 - x²/36 =1 y se obtiene: 

2. Obtener el centro, los vértices y los focos de la hipérbola del problema anterior.

Solución:

Considerando que GeoGebra asignó el nombre c a la hipérbola, se capturan los siguientes comandos, dando Enter, después de cada uno de ellos.

Centro(c)

Vértices(c)

Focos(c)

Los valores obtenidos se observan en la siguiente figura:

El centro tiene el nombre C, los vértices V1 y V2 y los focos F1 y F2.

3. Obtener la ecuación y la gráfica de la hipérbola cuyos focos son los puntos (-5,0) y (5,0) y sus vértices (-2.0) y (2,0)

Solución

La herramienta Hipérbola aparece en el séptimo grupo de herramientas (en el que están incluidas las cónicas) y solicita conocer los dos focos y en un punto de la curva.

Ya que cualquiera de los dos vértices es un punto de la curva, el procedimiento es el siguiente:

·       Se capturan las coordenadas de los focos F1= (-5,0) y F2= (5,0)

·       Se capturan las coordenadas de un vértice, por ejemplo V1=         (-2,0)

·       Se activa la herramienta Hipérbola y se hace clic, primero en cada uno de los focos y finalmente en el vértice.

Obsérvese que GeoGebra cambia la ecuación de forma.

4.  Obtener las asíntotas de la hipérbola cuya ecuación es (x+8)²/16 - (y-7)²/25 = 1

Solución

·       Se captura la ecuación en la forma (x+8)²/16 - (y-7)²/25 = 1

·       Se captura en la barra de Entrada el comando asíntota(c). Nótese que el comando está en singular.

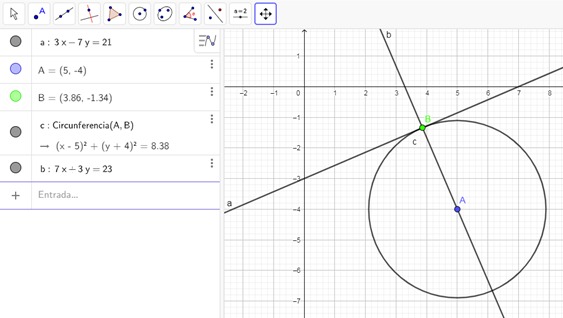
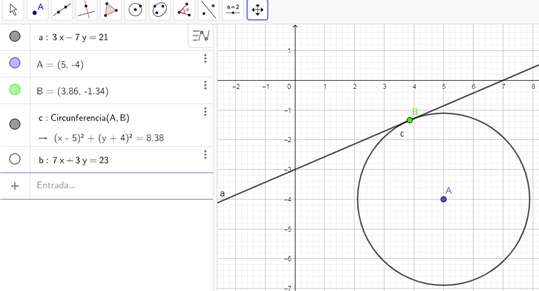
GeoGebra presenta las gráficas y ecuaciones de las asíntotas (a y b). 

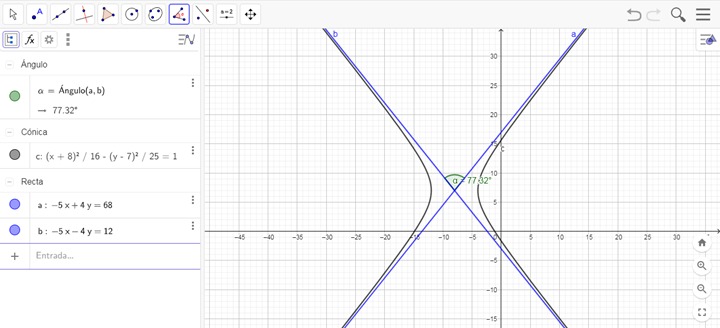
5. Obtener el ángulo entre las asíntotas del ejercicio anterior.

Solución:

·       La herramienta Ángulo que se observa en la siguiente figura, solicita tres puntos o dos rectas.

Al hacer clic en cada una de las rectas, en forma antihoraria, se obtiene el valor del ángulo.

ELIPSE

 1. Obtener la gráfica de la elipse cuya ecuación es (x-8)²/25 + (y-9)²/49=1

Solución:

Se captura la ecuación en la forma (x-8)²/25 + (y-9)²/49=1 y se obtiene:

2. Obtener el centro, los vértices y los focos de la elipse del problema anterior.

Solución:

·       Considerando que GeoGebra asignó el nombre c a la elipse, se capturan en Entrada los siguientes comandos, dando Enter, después de cada uno de ellos.

Centro(c)

Vértices(c)

Foco(c) = foco en singular

En este caso, el centro tiene el nombre C, los vértices son V1, V2, V3 y V4 y los focos F1 y F2.

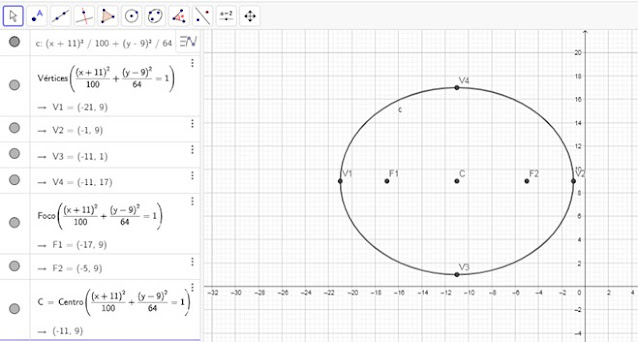
3. Obtener las longitudes del lado recto, del eje mayor y del eje menor de la elipse cuya ecuación es: (x+11)²/100 + (y-9)²/64=1 

Solución:

Se captura la ecuación en la forma (x+11)²/100 + (y-9)²/64=1 con lo que se obtiene la siguiente gráfica: 

Se obtienen el centro, vértices y focos, como en el problema anterior.

Se traza una recta paralela al eje Y que pase por el punto F.

Se obtienen los puntos de intersección entre esta recta y la elipse. 

Al trazar los segmentos entre los pares de puntos A y B, V1 y V2, y V3 y V4, ocultar la recta (a) y cambiar la ecuación a la forma ordinaria, se presenta la siguiente figura:

Las longitudes de estos tres segmentos son, respectivamente las del lado recto (i=12.8), del eje mayor (g=20) y del eje menor (h=16).

Bibliografía

Arriaga, J. G. & Ramírez, M. & Trujillo, J. R. (2012). Computación Básica. Libro de Texto, México: DENMS UAEMéx.

Goodman A. / Hirsch L. (1996). Álgebra y Trigonometría con Geometría Analítica. México: Prentice Hall

Lehmann, Ch. Geometría Analítica (1989). México: Limusa

Referencias electrónicas

http://wiki.geogebra.org/es/Manual